Maφjski vikend 2026 bo potekal od 16. do 18. januarja. Podroben program je na voljo spodaj.
- Petek, 16. 1. 2026 (predavalnica 2.02 in Zoom)
- 17.30 Matematično predavanje (prof. dr. Marjetka Knez): Uporabne krivulje
- 18.30 Fizikalno predavanje (prof. dr. Tomaž Zwitter): Planeti drugih zvezd in kaj bi se tam lahko našlo
- Sobota, 17. 1. 2026
- 8.45 Sprejem (predavalnica 2.02)
- 9.00 Delavnice v manjših skupinah*
- 12.30 Kosilo v kavarni Maφja
- 14.00 - 18.00 Mafijska avantura
- Nedelja, 18. 1. 2026
- 9.00 Delavnice v manjših skupinah*
- 12.30 Kosilo in zaključek v kavarni Maφja
* V soboto in nedeljo bodo na sporedu iste delavnice. Vsak dijak bo tako lahko izmed šestih ponujenih tem izbral dve.
O predavateljih:
prof. dr. Tomaž Zwitter
Tomaž Zwitter je redni profesor na oddelku za fiziko Fakultete za matematiko in fiziko. Raziskovalno se ukvarja z astrofiziko, zvezdami in sestavo ter razvojem naše galaksije v okviru več mednarodnih projektov, kot sta GALAH in Gaia-ESO. Prejel je tudi Zoisovo priznanje za pomembne dosežke (2013) in Zoisovo nagrado za vrhunske raziskovalne dosežke (2021).


prof. dr. Marjetka Knez
Marjetka Knez je redna profesorica na oddelku za matematiko Fakultete za matematiko in fiziko. Poučuje predmete iz numerične matematike, raziskovalno pa se med drugim ukvarja z numerično analizo, aproksimacijo krivulj in ploskev ter geometrijsko interpolacijo. Leta 2025 je za svoje izjemne zasluge prejela Zlato plaketo Univerze v Ljubljani.
Delavnice:
Laser in optični eksperimenti (Žiga Pušavec)

Laserji so eni izmed najbolj pogosto uporabljenih orodij v fizikalnih laboratorijih. Uporabljajo se za raziskovanje strukture snovi, vzbujanje atomskih prehodov, kot frekvenčna referenca pri natančnih meritvah, za obdelavo materialov, za komunikacijo … S fokusiranimi pulznimi laserji lahko npr. snov segrejemo do visoke temperature, na drugi strani pa lahko z ustrezno frekvenčno modulacijo laserske svetlobe snov ohladimo skoraj do absolutne ničle.
Na delavnici bomo najprej spoznali osnovne principe delovanja laserja, nato pa postavili nekaj enostavnih optičnih eksperimentov (kolimacija svetlobe, poravnava žarka, interferometer, optični resonator). Pou darek bo na praktičnem delu, kjer bodo udeleženci iz prve roke spoznali, kako poteka eksperimentalno delo v praksi. Za konec si bomo še pogledali prave eksperimente, ki se trenutno postavljajo v laboratoriju.
Kvantna mehanika in kvantno računalništvo (Urban Duh)

Kvantna mehanika je fizikalna teorija, ki opisuje obnašanje majhnih delcev. Ena izmed osnovnih lastnosti kvantne mehanike je nedeterminističnost, ki pa se je ne da razumeti samo s klasično verjetnostjo, ampak zanjo potrebujemo kompleksne verjetnostne amplitude. Na delavnici bomo spoznali kvantno mehaniko z vidika kvantnih bitov (kubitov) - najenostavnejših primerov kvantnih delcev. Preko njih bomo lahko razumeli kvantne meritve, interferenco in kvantno prepletenost. Kubiti so prav tako osnovni gradniki kvantnih računalnikov. Obravnavali bomo enostavne kvantne algoritme in videli, kako ter v katerih primerih so lahko ti učinkovitejši od klasičnih.
Delavnica je primerna za dijake višjih letnikov, delali bomo s kompleksnimi števili in vektorji (na nivoju 2. letnika gimnazije).
Fizika zvoka in glasbe (Domen Vaupotič)
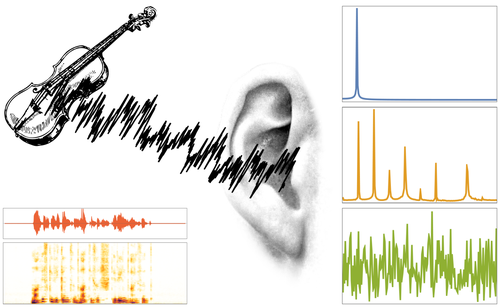
Zvok nas spremlja na vsakem koraku – v govoru, glasbi, naravnih pojavih in tehnologiji. Na delavnici bomo raziskovali zvok z vidika fizike in delovanja človeškega sluha. Spoznali bomo, kako nastane zvočno valovanje, s katerimi fizikalnimi količinami ga opišemo in kako vplivajo na to, kar slišimo. Posvetili se bomo Fourierovi transformaciji – matematičnemu orodju, s katerim lahko zapleten zvok razčlenimo na posamezne frekvenčne komponente in tako dobimo njegov zvočni spekter. Z uporabo mikrofona in računalniških orodij bomo analizirali zvoke različnih virov – od strun in glasbenih vilic do glasbil, zvočnikov in človeškega glasu. Primerjali bomo njihove spektre ter pojasnili, zakaj imajo različni zvoki različen značaj in zakaj nekateri zvenijo bolj prijetno kot drugi. Dotaknili se bomo tudi nastanka govora in vloge govoril pri oblikovanju glasov. Za konec si bomo ogledali spektrograme ter spoznali, kako lahko sodobne mobilne aplikacije, npr. Shazam, v nekaj sekundah prepoznajo skladbo.
Verjetnost (Luka Ponikvar in Anja Rupnik)
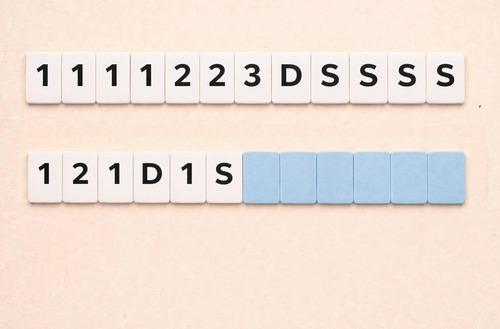
Na internetu najdete naslednjo igro na srečo z 12 ploščicami kot na sliki. V igri se ploščice obračajo od leve proti desni, dokler prvič ne naletimo na ploščico S (stop). Izplačilo igre je vsota števk na vidnih karticah, ki se pomnoži z 2, če je vidna ploščica D (double). Koliko ste pripravljeni plačati za igranje te igre?
Na predavanju bomo spoznali diskretne slučajne spremenljivke in z njihovo pomočjo odgovorili na zgornje vprašanje.
Problem razvoza (Luka Ponikvar in Anja Rupnik)
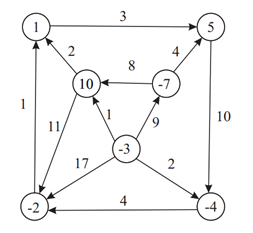
Ne sliki vidimo omrežje sestavljeno iz vozlišč in usmerjenih povezav. Vsako vozlišče ima znano ponudbo (število v vozlišču je negativno) oz. povpraševanje (število je pozitivno), vsaka povezava pa ima znano ceno.
Problem, ki ga rešujemo, je naslednji. Predstavljamo si, da so vozlišča s ponudbo pekarne, vozlišča s povpraševanjem šole, količino pa merimo z žemljicami. Vprašamo se, kaj je najmanjša cena, ki jo moramo plačati, da do vsake šole dostavimo želeno količino žemljic. Če žemljice peljemo po povezavi s ceno 3, bomo za vsako žemljico morali plačati 3 denarne enote.
Naš cilj bo najti postopek, ki bo za dano omrežje poiskal optimalno rešitev, torej najnižjo ceno in optimalni razvoz - navodila, po katerih povezavah peljemo žemljice od pekarn do šol. Med drugim si bomo pogledali tudi primere, ko je količina žemljic, ki jih lahko peljemo po določenih cestah navzdol ali navzgor omejena.
Tri stoletja enega izreka (Hana Ibrahimpašić)
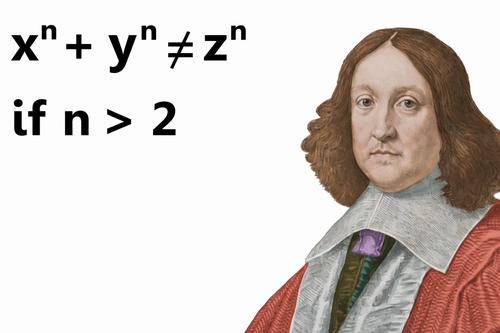
Fermatov zadnji izrek pravi, da pri nobenem naravnem številu \(n>2\) ne moremo najti treh pozitivnih celih števil \(x,y\) in \(z\), ki zadoščajo enačbi \(x^n+y^n=z^n\). Ta izrek je bil zapisan v 17. stoletju, njegov dokaz pa je matematikom kljuboval več kot 350 let. Skozi dolgo zgodovino iskanja dokaza so se pojavljali tudi poskusi, ki so temeljili na znanih lastnostih celih števil, npr. na enoličnem praštevilskem razcepu. Izkazalo se je, da v širših številskih strukturah takšne lastnosti ne moremo pričakovati.
Na delavnici si bomo ogledali, kako je bila ravno ta lastnost povezana z neuspešnostjo dokazovanja Fermatovega izreka, in motivirali nekaj pristopov, ki so se razvili kot odgovor na te težave.



